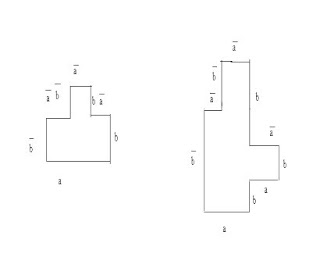Let n = |b(P )| be the length of the boundary word of P. In the following algorithm the indices of the boundary word b(P) (or  b for simplicity from here on when there are indices) are taken
modulo n. For example, the letter b[-1] is of course the letter b[n - 1].The boundary word b(P) is the sum of all the boundary segments PS=0; PH=0;
// Step 1: Searching correspondence between b[0] and b[i]
for i = 1 to n - 1
if b[0] = b[i] then
// Step 2: Propagation
// Searching the largest b[x1..y1] = b[x2..y2]
// b[x1..y1] containing 0 and b[x2..y2] containing i
x1 = 0; y1 = 1; x2 = i; y2 = i + 1;
while (b[x1 - 1] = b[y2]) {x1 = x1 - 1, y2 = y2 + 1}
while (b[y1] = b[x2 - 1]) {y1 = y1 + 1, x2 = x2 - 1}
// end of Step 2
U = b[y1 + 1..x2 - 1]; V = b[y2 + 1..x1 - 1];
if |U | = |V | then
if U = V then PS=PS+1 // Step 3: Pseudo-square
PH=PH+ KMP(U , V V ) // Step 4: Pseudo-hexagon
end if
end if
end for

EXPLANATION OF THE ALGORITHM STEP BY STEP

Step 1
For each position i from 1 to n - 1, we try to match with the complementary letter of value b[0],i.e. we try to find all the positions of value (0).

Step 2
We make a propagation (scanning back and forth the boundary words) in order to have two sides in correspondence of maximal length. In other words, for each position of value b[0], we find by propagation two  complementary words X and X on the boundary word starting from X = b[0] and X = b[0] and extending the pair of complementary words (X, X ) in order to find the longest X. Then by this method we find a factorization of b(P ) by X ·U ·X · V

Step 3
We now check that the remaining sides U and V have same length. And we answer that the polyomino is a pseudo-square if U = V that is if we have found a factorization on X · Y · X ·Y with Y = U.

Step 4
We check if the polyomino is a pseudo-hexagon by searching four more sides in two-by-two correspondence, that is the factorization U = Y · Z and V = Y · Z. We use the following
property: if such factorization exists, it is provided by an occurrence of the word U = Z · Y in V V = Y · Z · Y · Z. . Thus, this algorithm decides whether a given polyomino tiles
a plane or not.
COMPLEXITY OF THE ALGORITHM
In the first step the algorithm tries to find all the positions of value b(0) with a complexity O(n).In step 2 the propagations gives complexity O(n).Thus the total complexity for steps 1
and 2 is O(n*n).that are pseudo-sqares and pseudohexagons.Step 3 gives a complexity of O(n).But it is just a continuation of step 2,so complexities are added.Thus the total
complexities for steps 1, 2 and 3 is O (n(n+n))= O(n^2).

CONCLUSION/FUTURE WORK
I would like to conclude by saying that this algorithm has been tested for polyominoes that are pseudo-sqares and pseudohexagons.I shall try to make this more effective.I would also
like to use this knowledge to research periodic tilings and design an algorithm to decide whether a given polyomino admits a periodic tiling of the plane.


ACKNOWLEDGMENT
I would like to thank Prof. Samaresh Chatterji, Prof.John Steinberg of University of British Columbia, Prof.Casey Mann of The University of Texas, and Joseph S. Myers for their invaluable support and encouragement.


REFERENCES

[1] Brass Peter, Moser William and Pach Janos , “Research Problems in Discrete Geometry"
[2] Internet :http://www.math.sunysb.edu/~tony/und_res_projects.html
http://www.srcf.ucam.org/~jsm28/tiling/
http://math.uttyl.edu/cmann/math/research/research.htm
[3] Grunbaum and Sheppard , “Theory of Tilings”